 |
| James Clerk Maxwell |
Campos elétricos e magnéticos
Antes de iniciar nossos estudos sobre as ondas eletromagnéticas e partir para as equações de Maxwell, precisamos entender bem os conceitos de campos elétricos e magnéticos.Podemos ver campos elétricos e magnéticos como quantidades vetoriais, que possuem tanto direção com magnitude (um módulo, um valor real).
E são essas relações, entre os campos elétrico e magnético, bem como a relação entre cargas e correntes, que associadas ao conceito de ondas eletromagnéticas, são estudadas pela física através das famosas equações de Maxwell, que podem ser descritas tanto na forma integral quanto diferencial.
Mas embora seja possível representar as leis de Maxwell em ambos tipos de equações, o uso dessas formas não é 'irrestrito', e usamos dependendo do problema em questão. Por exemplo, dependendo da geometria da questão, das fontes ou dos campos, podemos usar uma abordagem ou outra das equações.
Equações de Maxwell na forma integral e diferencial
Equações de Maxwell na forma de integral
Nesta forma, as equações são bem mais gerais que na forma diferencial, que veremos a seguir.Usamos as equações nesta forma para trabalhar as relações vetoriais de campo, densidade de corrente e de carga no espaço.
São usadas em todos os tipos de fenômenos e situações que envolvem o eletromagnetismo, mas somente no mundo macroscópico.
Ou seja, usamos as equações de Maxwell na forma de integral para trabalhar em grandes dimensões, que não são dimensões atômicas.
Equações de Maxwell na forma diferencial
Assim como na forma integral, servem para se trabalhar as relações dos vetores de campo, de densidade de corrente e de carga, no espaço e no tempo.Este tipo de equações são um pouco mais complicadas de se trabalharem, pois exigem que os campos sejam 'bem comportados'.
Se você lembrar bem de seus estudos de derivadas, vai lembrar que para que ocorra o processo de derivação é necessário que as funções sejam continuas, com derivadas também contínuas, e isso nem sempre ocorre em uma situação real, nos campos, onde nem sempre estes campos são descritos por funções contínuas, de valor único e limitados.
As equações de Maxwell na forma diferencial são geralmente usadas em problemas que possuem simetria geométrica (esférica, cilíndrica etc).
Porém, quando existe transição entre os meios, os campos são descontínuos, daí pode ocorrer distribuição descontínua de cargas e de corrente. Estudaremos mais sobre isso quando falarmos de condições de fronteiras.
Teorema da Divergência e Teorema de Stokes
Quando falarmos, mais a frente, sobre cada uma das equações de Maxwell, vamos mostrar tanto as formas integral como diferencial. Por isso, vamos aprender agora dois teoremas que irão nos ajudar a obter a forma diferencial a partir da forma integral: os teoremas da divergência e de Stokes.Teorema da Divergência
O teorema da divergência estabelece que, se v é um volume limitado por uma superfície s, e se V é um campo vetorial com derivadas parciais contínuas na região definida pela superfície s, então:"A integral da componente normal de qualquer campo vetorial, sobre uma superfície fechada, é igual à integral da divergência desse campo através do volume envolvido pela superfície fechada."
Na forma matemática temos
Teorema de Stokes
O teorema de Stokes estabelece que:"A integral da componente tangente de qualquer campo vetorial, sobre uma linha fechada, é igual à integral da componente normal do rotacional do campo vetorial sobre a superfície."
Na forma matemática temos:
Lei de Faraday
Iniciando nossos estudos sobre as equações de Maxwell, vamos iniciar pela lei de Faraday, que estabelece:"A força eletromotriz ( fem) total induzida num circuito fechado é igual a taxa de decréscimo, em relação ao tempo, do fluxo magnético total que enlaça o circuito."
A sua forma matemática integral é:
E aplicando o Teorema de Stokes nessa equação, obtemos a equação da Lei de Faraday na forma diferencial:
Os elementos destas equações estão definidos na figura seguinte:
Lei de Ampère
A lei de Ampère diz que:
"A integral de linha de H, ao longo de um único caminho fechado, força magneto-motriz, é igual a corrente envolvida pelo caminho."
A sua forma matemática, na forma integral, é:
O segundo termo, do lado direito da equação da Lei de Ampère, é a corrente de deslocamento, termo proposto por Maxwell para satisfazer a equação da conservação de carga, este termo implica na existência de uma onda eletromagnética.
Aplicando Stokes novamente na Lei de Ampère na forma de integral, conseguimos facilmente ter a forma diferencial:
Onde os elementos destas equações estão ilustrados na figura seguinte:
Lei de Gauss para campos elétricos
O enunciado da lei de Gauss para campos elétricos é"A integral de superfície da componente normal da densidade de fluxo elétrico D, sobre qualquer superfície fechada, é igual à carga englobada por esta superfície."A forma matemática desta Lei, proposta pelo matemático Gauss, na forma de integral é:
E na forma diferencial:
E sua geometria, bem como seus elementos, são representados pela seguinte figura:
Lei de Gauss para campos magnéticos
Estabelece que o fluxo magnético líquido (positivo ou negativo) que emana de qualquer superfície fechada s, no espaço, é sempre zero, isto é, o fluxo magnético não tem fonte, as linhas do campo B não podem ter início ou fim, como é mostrado na figura (até agora, não foi observado a existência de fonte (cargas ou corrente magnética) de campo magnético.Na forma de integral, a equação é:
E na diferencial:
Os seguintes links irão auxiliá-los nos seus estudos sobre Equações de Maxwell, Teorema de Stokes, Teorema da Divergência e como calcular rotacional












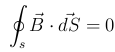

Nenhum comentário:
Postar um comentário